统计学习方法笔记(1)——统计学习及监督学习概论
前言
机器学习入门的战线可以说是拉的很长,想着要早早学完理论,实战数据科学赛事,为研究生打好基础,但到现在也依旧是门外小白一枚。
总是会在浩如烟海的学习资料里翻来覆去,西瓜书只翻了三四章,便看到网上说西瓜书前期学习作为参考资料更好,具体的公式推导不详细,不适合作为入门自学读物,自学搞懂原理中文教材还是选李航教授的《统计学习方法》比较好,便有些犹疑是否要先学完西瓜书。加之刚好看到Datawhale群里小伙伴开了个统计学习群,于是就给自己开了这个新坑,希望能完整系统学完这本《统计学习方法》。
笔记以《统计学习方法》第二版为主线,辅以学习过程中遇到的一些困惑点的进一步深挖。考虑到按自己传统的笔记方式很可能只是拎各种概念和方法,缺乏自己的深度思考,写完自己查阅也不方便,内容会很冗长,参考了群友Terr的笔记方式,决定尽可能精炼内容,以Q&A+思维导图的方式来辅助后续的学习,后续学习有新的思考也会逐渐补充至Q&A中。
1 统计学习及监督学习概论
思维导图梳理
因为内容很多,把整章划分成了四个部分。
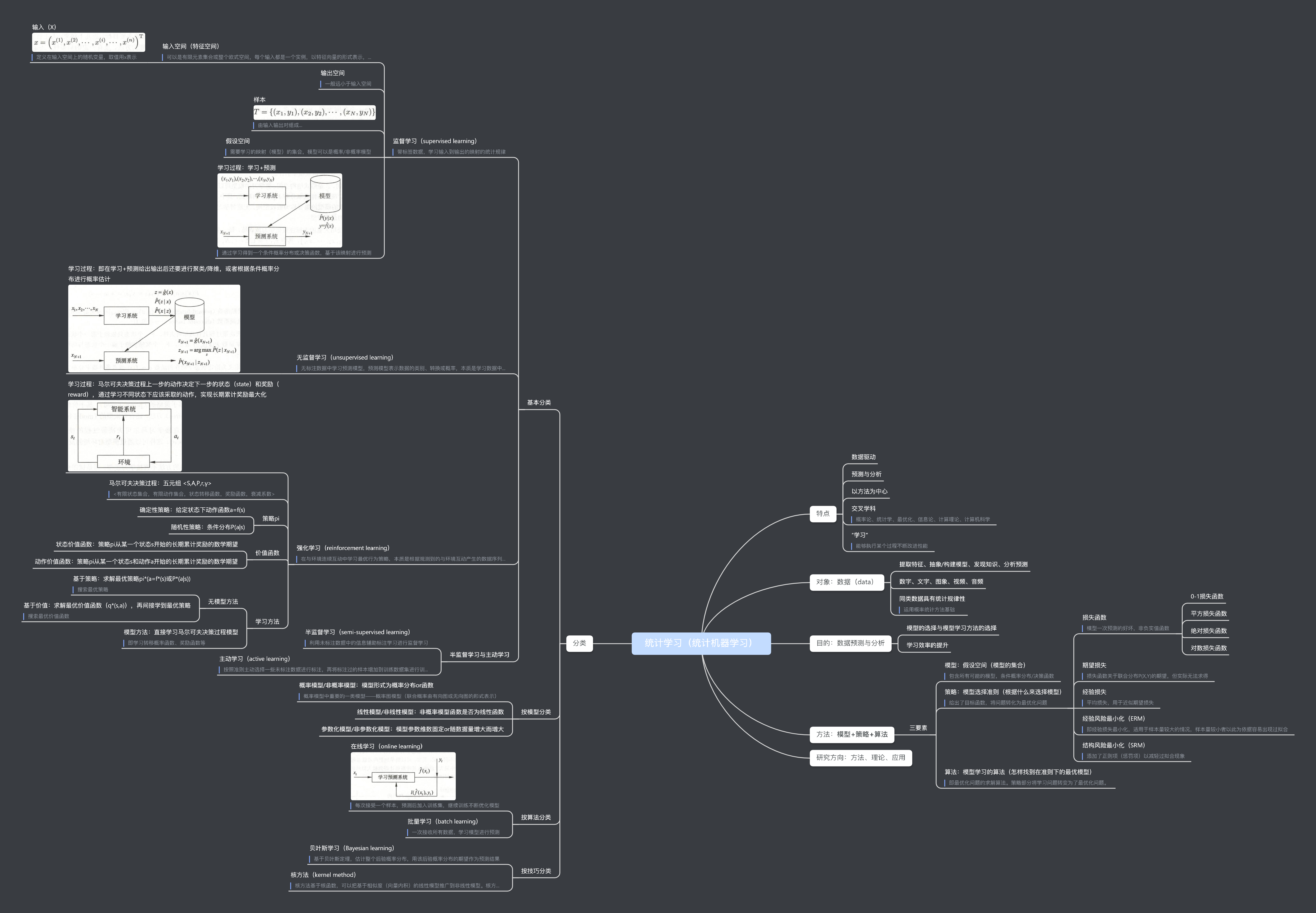



1.1 统计学习
Q1 统计学习、统计学和机器学习到底是什么关系?
每次看到「统计学习」四个字都会困惑,统计学就统计学,统计学习又是什么?《统计学习方法》一书为什么又是机器学习的入门书?加之专业课学习计量经济学后,发现机器学习方法有很多都是与统计学习方法一致的,愈发困惑。
书中没有对二者加以明确的区分,但貌似并没有将二者对等:
统计学习(statistical learning)是关于计算机基于数据构建概率统计模型,并运用模型对数据进行预测和分析的学科。统计学习也称统计机器学习(statistical machine learning)。
现在,当人们提及机器学习时,往往是指统计机器学习。所以可以认为本书介绍的是机器学习方法。
个人理解:
统计学习区别于统计学,但其根基在于概率论与统计学,是机器学习的先决条件。统计学的目标更多地在于假设检验和因果推断,侧重于寻找已有数据中各变量逻辑上的因果关系(二者之间有逻辑联系),关心推断或预测的置信度,实际处理中更关注统计量服从什么分布、假设检验是否显著、模型拟合是否合理等问题;统计学习则主要是利用建立的统计模型进行预测和分析,更侧重于数据之间的相关关系(即在数学意义上可以观察到二者存在联系,线性/非线性关系)。
统计注重inference(推论),而ML注重prediction(预测)
后续,查阅了维基百科,科学家们更多地认为统计学习是机器学习和统计学的交叉领域。且从机器学习发展里程来看,机器学习最早起源于符号学习,到20世纪七十年代在其基础上发展出了统计学习,而与此同时,连接主义派兴起,发展出了以神经网络为代表的基于连接的机器学习。因此,个人认为统计学习和机器学习二者不能等同。除统计学习之外,还应包括以ANN为代表的神经网络与深度学习。
具体关系参考了一下知乎ST ym给出的关系图(可能不一定正确):
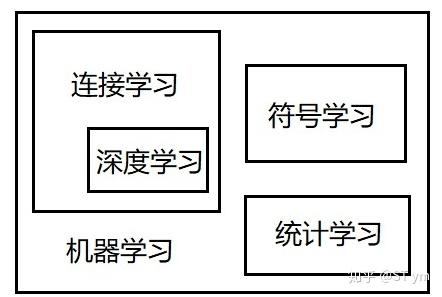
1.2 统计学习的分类
Q2 频率学派和贝叶斯学派的区别?
二者隶属于统计学,是统计学的两大学派,代表两套不同的统计推断体系。
核心区别在于对统计参数的看法。统计参数是对未知总体分布的一种描述,统计推断即通过已有样本来对总体的分布进行推断,估计总体的参数。
频率派认为概率是客观的,事件本身就具有随机性,因此,参数是客观存在的,是一个确定的值,只要找到这个参数,就能够描绘随机事件(现象),了解到总体的分布。
贝叶斯学派则认为概率是主观的,事件本身不具有随机性,随机性来自于不同观察者对事件发生的主观判断,统计参数也是随机的,因为我们不能观察到整体,我们并不能知道参数的具体值,这和一个随机数没有区别,因此参数空间里的每个值都可能是真实的值,但是概率不同。
因此,频率派最常关心的是似然函数和置信区间,即有多少的把握圈出那个正确的参数;而贝叶斯派最常关心的是后验分布和先验分布,利用二者来寻找参数的分布。(对贝叶斯估计的理解可以看下一个问题)
Q3 极大似然估计和贝叶斯估计的区别?
大二上学的概率论与数理统计,印象不够深了,上课只讲了极大似然估计,没有提及贝叶斯估计方法,这里重新做一个整理。
似然与概率
- 似然(likelihood):已知结果,对参数是某个值的可能性预测
- 概率(probability):已知参数,对结果可能性的预测
In statistics, the likelihood function (often simply called the likelihood) measures the goodness of fit of a statistical model to a sample of data for given values of the unknown parameters. It is formed from the joint probability distribution of the sample, but viewed and used as a function of the parameters only, thus treating the random variables as fixed at the observed values.
似然函数针对给定的未知参数值来衡量统计模型与数据样本的拟合优度。 它是由样本的联合概率分布形成的,但是仅作为参数的函数进行查看和使用,它将随机变量固定为观察值。
似然与概率其实都是围绕$P(X|\theta)$展开的。
- 当固定$\theta$,则该函数为概率函数,表示随机变量$X$为不同值的概率。
- 当固定$x$,则该函数为似然函数,一般写作$L(\theta|x)$或$L(x;\theta)$,表示不同$\theta$下,$X=x$的概率
极大似然估计(MLE)
基于频率学派,既然要找到那个实际的参数,那么使得观测数据(样本)发生概率最大的参数就是最好的参数。
即:使得似然函数值在现有$x$的情况下最大的$\theta$值。
$$
\max_\theta L(X;\theta)
$$
由于样本之间满足独立同分布假设,似然函数可以通过样本概率函数的乘积得到:
$$
L(X;\theta)=\prod_{i=0}^nP(x_i|\theta)
$$
为了求解方便,通常会将似然函数转成对数似然函数,然后再求解。对数函数并不影响函数的凹凸性。
最大后验估计(MAP)
相比于极大似然估计,最大后验概率估计认为$\theta$是一个随机变量,满足一定分布(先验分布),求解时除考虑似然函数$P(X|\theta)$外,还要考虑$P(\theta)$。
即:选择使$P(X|\theta)P(\theta)$最大的$\theta$。
$$
\arg\min_{\theta}P(X|\theta)P(\theta)
$$
与极大似然估计的思想是一致的,寻找使当前事件发生可能性最大的参数值,只不过多考虑了先验分布,吸收了贝叶斯学派的部分思想。这里的$P(\theta)$需要进行描述(定义),由于最终参数的确定需依赖于先验分布,因此,受主观影响较大。
最大后验概率估计可以看作是正则化的最大似然估计,当然机器学习或深度学习中的正则项通常是加法,而在最大后验概率估计中采用的是乘法,$P(\theta)$是正则项。在最大似然估计中,由于认为$\theta$是固定的,因此$P(\theta)=1$。
实际上,由于$P(X)$已知,最大化的其实是$\theta$的后验概率$P(\theta|X)$,这就是其名字的来源。
$$
\arg\min_{\theta} P(\theta|X)=\arg\min_{\theta}\frac{P(X|\theta)P(\theta)}{P(X)}\propto\arg\min_{\theta}P(X|\theta)P(\theta)
$$
贝叶斯估计
最大后验估计的扩展,贝叶斯估计同样假定$\theta$是一个随机变量,但贝叶斯估计并不是直接估计出$\theta$的某个特定值,而是估计$\theta$的分布。在已知$X$的情况下,描述$\theta$的分布即描述后验概率$P(\theta|X)$。
贝叶斯估计中,先验分布$P(X)$是不可忽略的,可以使用全概率公式求得:
$$
P(\theta|X)=\frac{P(X|\theta)P(\theta)}{P(X)}=\frac{P(X|\theta)P(\theta)}{\int_\Theta P(X|\theta)P(\theta)d\theta}
$$
贝叶斯估计的求解非常复杂,因此选择合适的先验分布就非常重要。一般来说,计算积分$\int_\Theta P(X|\theta)P(\theta)d\theta$是不可能的。
如果后验分布的范围较窄,则估计值的准确度相对较高,反之,如果后验分布的范围较广,则估计值的准确度就较低。
小结一下
- 都是参数估计的方法,即预先知道/假设样本的分布形式,只是一些参数未知。
- 极大似然估计和最大后验估计都是点估计。即把参数看成未知常数,通过最大化似然和后验概率实现。
- 极大似然估计和最大后验估计都在寻找使当前事件发生可能性最大的参数值。最大似然最简单,只需找到使得样本似然函数最大的参数。而最大后验优化似然函数为似然 * 先验概率,考虑了参数的先验概率,多了一个先验概率项。
- 贝叶斯估计把参数看成一个随机变量,属于分布估计。贝叶斯是最大后验函数的扩展,和二者最大的不同在于,其最终得到的是一个参数分布(后验分布)。
因此,可以认为,极大似然估计是频率派的方法,贝叶斯估计是贝叶斯学派的方法。
尽管最大后验估计与贝叶斯统计共享先验分布的使用,通常并不认为它是一种贝叶斯方法,这是因为最大后验估计是点估计,然而贝叶斯方法的特点是使用这些分布来总结数据、得到推论。
Q4 怎么理解极大似然估计是经验风险最小化的一个例子,最大后验估计是结构风险最小化的一个例子?
先不管证明,基于Q3里对三种参数估计方法的介绍,可以这样理解,极大似然寻找使当前已观察到样本可能性最大的参数。而经验风险最小化,其实就是寻找预测结果与真实结果差异可能性最小的参数。两者在思想上是一致的。结构风险最小化在经验风险最小化的基础上考虑了正则项(罚项),这和最大后验概率估计在最大似然估计多考虑了参数的先验分布类似,都额外考虑了参数自身的特征。
形式上,最大后验概率/极大似然取对数后,乘法就变成了加法,形式也基本一致了。
下面对其作数学证明(课后习题2):
对数损失函数:
$$
L(Y,P(Y|X))=-\log P(Y|X)
$$
经验风险函数式:
$$
\begin{align}
R_\text{erm}(P_\theta)=&\min_{P_\theta\in\mathcal{F}}\frac{1}{N}\sum_{i=1}^NL(y_i,P_\theta(y_i|x_i)) \\
=&-\min_{P_\theta\in\mathcal{F}}\frac{1}{N}\log(\prod_{i=1}^NP_\theta(y_i|x_i)) \\
=&\frac{1}{N}\max_{P_\theta\in\mathcal{F}}\log(\prod_{i=1}^NP_\theta(y_i|x_i))
\end{align}
$$
相当于极大似然估计(最大化对数似然函数):
$$
\max_{\theta\in\mathrm{R}^n}\log(\prod_{i=1}^NP_\theta(y_i|x_i))
$$
得证。
同理,当模型复杂度由模型的先验条件表示时,结构风险表达式多添加了一个正则项$P(\theta)$,由于对数函数将加法转化为乘法,最终形式也与最大后验概率函数相同。
1.3 统计学习三要素
Q4 优化和机器学习为什么总是有交叉的内容?
因为专业涉及优化运筹,会需要学习相关的优化算法,之前学习的时候发现很多算法是通用的,不太明白优化和机器学习的关系,这个问题,书里给了很好的解答。
通过确定统计学习三要素之一的策略(经验风险最小化和结构风险最小化),机器学习问题就转化为了最优化问题。即:当我们确定了选择最优模型的准则,就已经确定了最优化问题里的目标函数,后续要解决的就是如何求解得到这个最优模型的问题。(标准最优化)
因此就会用到非线性规划中的梯度下降法以及其他优化算法。
Wikipedia在机器学习词条中这样写道:
The study of mathematical optimization(最优化) delivers methods, theory and application domains to the field of machine learning.
当然,最优化问题更倾向于得到一个精确解,机器学习问题则更关注模型最终的学习效果,即对模型在未知样本的代价上的最小化。换句话说,优化是机器学习的重要内容和过程,它能够使得其在给定的策略下学习到一个好的模型。然后我们再基于这个模型在新数据上进行预测,来得到我们需要的结果。
The difference between the two fields arises from the goal of generalization: while optimization algorithms can minimize the loss on a training set, machine learning is concerned with minimizing the loss on unseen samples.
1.7 生成模型与判别模型
Q5 生成方法中的隐变量是什么意思?
隐变量(latent variable),即那些不能被直接观察到,但可以通过其他可观测变量的特征间接推断出的变量。
举个栗子,经济学上的生活质量就可以视作隐变量,无法直接被衡量,但可以借助其他可观察变量来推断它, 衡量生活质量的可观测变量包括财富、就业、环境、身心健康、教育、娱乐和休闲时间以及社会归属感等等。
In statistics, latent variables are variables that are not directly observed but are rather inferred (through a mathematical model) from other variables that are observed (directly measured). Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models.
有一系列不同的模型和方法可以利用隐变量,或允许对隐变量进行推断,如隐马尔可夫模型、因子分析。推断隐变量的方法往往会涉及降维,通过对在高维空间上的特征进行降维,就可以得到隐含的隐变量。
Q6 标注问题与分类问题的关系or区别?
二者的输出变量都只能取有限个离散值,区别在于输入输出的单位:
- 分类(classification):构建一对一的映射,以单个样本为单位进行输入输出。模型形式表示为为$P(Y|X)$或$Y=f(X)$
- 标注(tagging):分类问题的推广,构建多对多的映射,以序列为单位进行输入输出。模型形式表示为条件概率分布$P(Y^{(1)},Y^{(2)},\dots,Y^{(n)}|X^{(1)},X^{(2)},\dots,X^{(n)})$。较多应用于信息抽取与自然语言处理。
参考资料
[1] 维基百科相应词条
[2] 传统的统计和机器学习的区别和联系是什么? - PengyuCheng的回答 - 知乎
[3] 贝叶斯学派与频率学派有何不同? - Xiangyu Wang的回答 - 知乎
[4] *贝叶斯估计、最大似然估计、最大后验概率估计【写的非常清楚全面,梳理了ML中常用的概率统计知识】